Multilayer Perceptrons II

Prof. Forrest Davis

Outline

• Errors as Changing Connections
• Chain Rule and Derivation of Perceptron Learning Rule
• Backward and Backpropagation

Errors as Changing Connections

• Reconsider a perceptron, where $t(x)$ is 0 if $x<0$ and 1 otherwise.

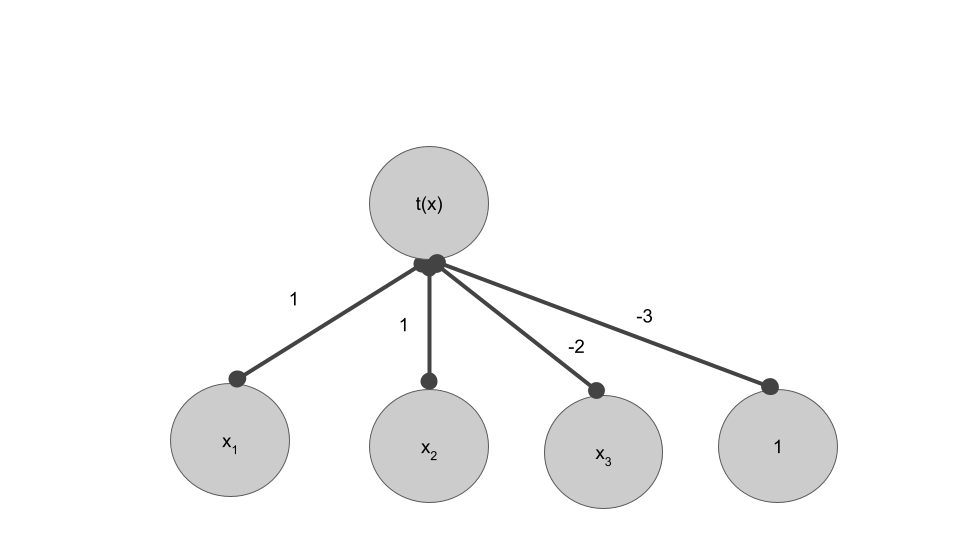
• Your input is $[-1, -2, 3]$ and your desired output is 1

Question: What is your current model's prediction

Answer $$t(-1-2-6-3) = 0$$

Question: How should we update our weights

Answer

Decrease weights on $x_1$ and $x_2$ and increase weights on $x_3$ and the bias.

Chain Rule of Calculus and Derivation of Perceptron Learning Rule

• Recall (or learn) the chain rle of calculus.

  • Suppose we have a function $F(x) = f(g(x))$
  • The derivative of $F(x)$ wrt $x$ is defined as $$ F'(x) = f'(g(x))g'(x)$$
  • if we define $y = f(u)$ and $u=g(x)$ then we can express this derivative as $$ \frac{d_y}{d_x} = \frac{d_y}{d_u} \frac{d_u}{d_x} $$

• Suppose $R(z) = \sqrt{5z-8}$

• Further, consider

  • $f(u) = \sqrt{u}$
  • $f'(u) = \frac{1}{2}\sqrt{u}^{-\frac{1}{2}}$
  • $g(z) = 5z-8$
  • $g'(z) = 5$

Question Use the chain rule to find $R'(z)$

Answer

$$R'(z) = \frac{1}{2}(5z-8)^{-\frac{1}{2}}5 $$

Question Consider $R(x) = g(x)^n$. Work through the chian rule to give an expression for $R'(x)$

Answer

$$R'(x) = n g(x)^{n-1} g'(x)$$

Question: Derive our update rule. Consider a modified MSE cost function

$$L = \frac{1}{2m}\sum_{i=1}^m (y^{(i)}-\hat{y}^{(i)})^2 $$

• To derive our update rule, do the following

1. Recall the general form (using $w_i$) for our forward pass
2. Use chain rule to find $\frac{\partial L}{\partial w_1}$, $\frac{\partial L}{\partial w_2}$, $\frac{\partial L}{\partial w_3}$, $\frac{\partial L}{\partial b}$. Note, ignore $t()$ when calculating gradients.
3. Change weights ($w_1$, $w_2$, $w_3$, $b$) in accordance to your findings (assuming a learning rate of 1)

Answer

1. $\hat{y} = t(w_1x_1+w_2x_2+w_3x_3+b)$

2. \begin{align} \frac{\partial L}{\partial w_1} &= \frac{\partial L}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial w_1} \\ \frac{\partial L}{\partial \hat{y}} &= 2*\frac{1}{2}(y^{(i)}-\hat{y}^{(i)})^{2-1}\hat{y}'\\ &= (y^{(i)}-\hat{y}^{(i)})^1 * -1 \\ \frac{\partial \hat{y}}{\partial w_1} &= x_1\\ \therefore \frac{\partial L}{\partial w_1} &= - (y^{(i)}-\hat{y}^{(i)}) x_1 \end{align}

Similarly, \begin{align} \frac{\partial L}{\partial w_2} &= - (y^{(i)}-\hat{y}^{(i)}) x_2\\ \frac{\partial L}{\partial w_3} &= - (y^{(i)}-\hat{y}^{(i)}) x_3\\ \frac{\partial L}{\partial b} &= - (y^{(i)}-\hat{y}^{(i)}) \end{align}

3. Substituting values \begin{align} \frac{\partial L}{\partial w_1} &= - (1-0) (-1) = 1 \\ \frac{\partial L}{\partial w_2} &= 2 \\ \frac{\partial L}{\partial w_3} &= -3\\ \frac{\partial L}{\partial b} &= -1 \end{align}

We want to reverse sign. Why? We decided before that we want to decrease $w_1$/$w_2$ and increase $w_3$/$b$. These are the opposite of the values we are seeing.

We can use a familiar update rule $\theta^{\textrm{new}} = \theta^{\textrm{old}} - \eta \nabla_\theta L$. So our new network is:

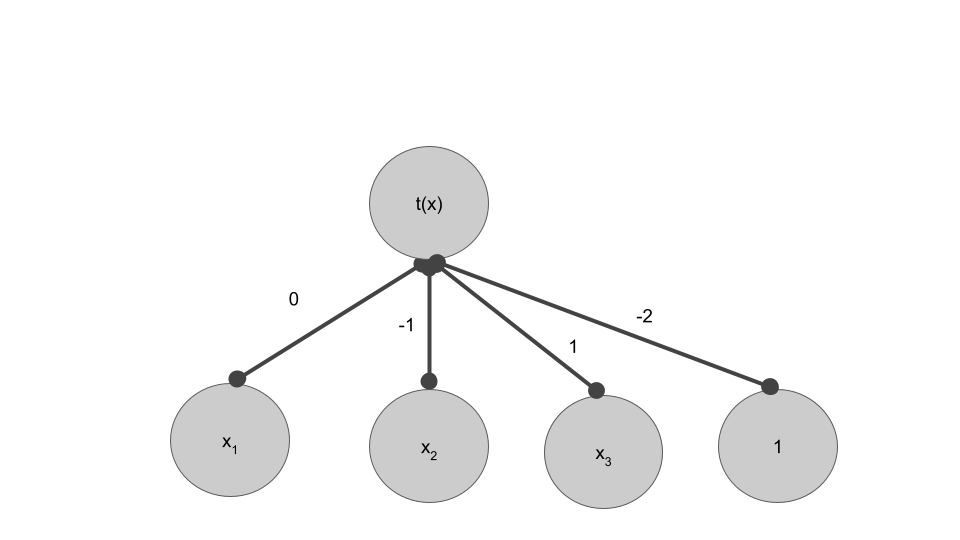
which gives us a new preidction of $t(2+3-2) = 1$ :)

Backward and Backpropagation

• Consider this multi-layer neural network, graphed here eliding connection weight labels and the bias for visual simplicity

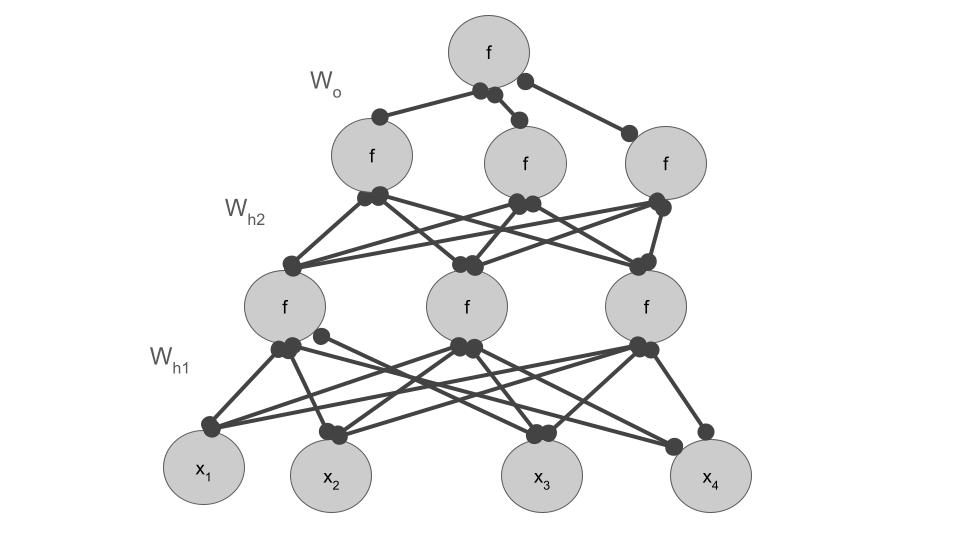
Question GIve the general expression for this network assuming,

• $W_{h_1}$ is the weight matrix mapping input to hidden layer 1
• $W_{h_2}$ is the weight matrix mapping hidden layer 1 to hidden layer 2
• $W_{o}$ is the weight matrix mapping hidden layer 2 to the output
• and $b_{h_1}$, $b_{h_2}$, $b_{h_2}$ are the relevant biases

Answer

$$ O = f(W_o^T f(W_{h_2}^T f( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) +b_{h_2}) $$

Question: Calculate the gradient wrt to $W_{h_o}$, $W_{h_2}$, $W_{h_1}$.

Hints:

• Treat $W_{h_o}$, $W_{h_2}$, $W_{h_1}$ as if they were scalars
• First tell me $\frac{\partial z}{\partial w}$ where $z = 3f(g(wx+4)+6)$

Answer

\begin{align} \frac{\partial z}{\partial w} &= \frac{\partial z}{\partial f} \frac{\partial f}{\partial g} \frac{\partial g}{\partial w} \\ &= 3xf'(g(wx+4)+6)g'(wx+4)\\ \end{align}

Answer

\begin{align} O &= f(W_o^T f(W_{h_2}^T f( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) +b_{h_2})\\ \frac{\partial O}{\partial W_o} &= f'(W_o^T f(W_{h_2}^Tf( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) +b_{h_2}) \\ &\cdot f(W_{h_2}^T f( W_{h_1}^Tx+b_{h_1})+ b_{h_2})\\ \frac{\partial O}{\partial W_{h_2}} &= f'(W_o^T f(W_{h_2}^Tf( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) +b_{h_2}) \\ &\cdot W_o^T f'(W_{h_2}^T f( W_{h_1}^Tx+b_{h_1})+ b_{h_2})\\ &\cdot f( W_{h_1}^Tx+b_{h_1})\\ \frac{\partial O}{\partial W_{h_1}} &= f'(W_o^T f(W_{h_2}^Tf( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) +b_{h_2}) \\ &\cdot W_o^T f'(W_{h_2}^T f( W_{h_1}^Tx+b_{h_1})+ b_{h_2})\\ &\cdot W_{h_2}^Tf'( W_{h_1}^Tx+b_{h_1}) \cdot x\\ \end{align}

Question Beyond this being tediuous, what are some computational limitations in updating each parameter (e.g., $W_o$) by evaluating these expressions? Consider what you have to compute.

Answer

There are many repeated terms. That means I rec-calculate the same values again and again. As I add more layers, the number of duplicate calculations grows!

Question Consider the following modified version of $\frac{\partial O}{\partial W_{h_2}}$. Tell me what A, B, C, A', B', and C' expand to and give me the modified versions of $\frac{\partial O}{\partial W_{h_1}}$ and $\frac{\partial O}{\partial W_{o}}$.

$$\frac{\partial O}{\partial W_{h_2}} = A'W_oB'C $$

Answer

\begin{align} A' &= f'(W_o^T f(W_{h_2}^Tf( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) +b_{h_2}) \\ A &= f(W_o^T f(W_{h_2}^Tf( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) +b_{h_2}) \\ B' &= f'(W_{h_2}^Tf( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) \\ B &= f(W_{h_2}^Tf( W_{h_1}^Tx+b_{h_1})+ b_{h_2}) \\ C' &= f'( W_{h_1}^Tx+b_{h_1}) \\ C &= f( W_{h_1}^Tx+b_{h_1}) \\ \frac{\partial O}{\partial W_{h_2}} &= A'W_oB'C \\ \frac{\partial O}{\partial W_{h_1}} &= A'W_oB'W_{h_2}C' x \\ \frac{\partial O}{\partial W_{o}} &= A'B \\ \end{align}

Question Reconsider our graph. Label it with where A, B, and C are calculated.

Answer

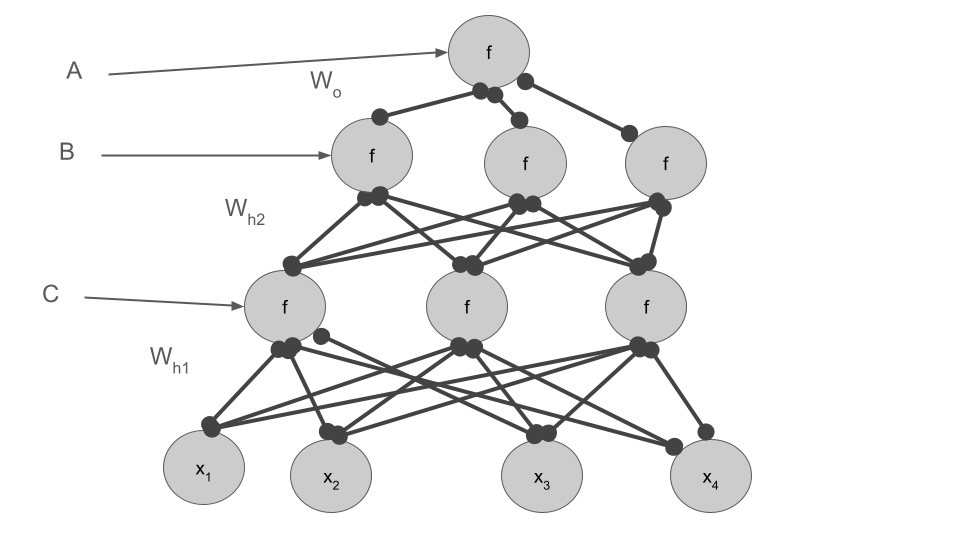
Question Finally, let's add in our loss (modified MSE for now)

$$L = \frac{1}{2m}\sum_{i=1}^m (y^{(i)}-\hat{y}^{(i)})^2 $$

Tell me $\frac{\partial L}{\partial W_o}$

Answer

\begin{align} \frac{\partial L}{\partial W_o} &= \frac{\partial L}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial W_o}\\ &= -\frac{1}{m}\sum_{i=1}^m (y^{(i)}-\hat{y}^{(i)}) A'B\\ \end{align}

Question Can you think of a better algorithm for calculating the gradients without repeating computations? Consider when you know A, B, C.

Answer

Backpropagation:

1. Calculate A, B, C (and gradients) w/ forward pass (i.e. generation of $\hat{y}$)
2. Calculate $-\frac{1}{m}\sum_{i=1}^m (y^{(i)}-\hat{y}^{(i)})$
3. Apply this to gradients calculated earlier by going backward through the network

You just derived Backpropagation!