Multilayer Perceptrons II

Prof. Forrest Davis

Outline

• Errors as Changing Connections
• Chain Rule and Derivation of Perceptron Learning Rule
• Backward and Backpropagation

Errors as Changing Connections

• Reconsider a perceptron, where $t(x)$ is 0 if $x<0$ and 1 otherwise.

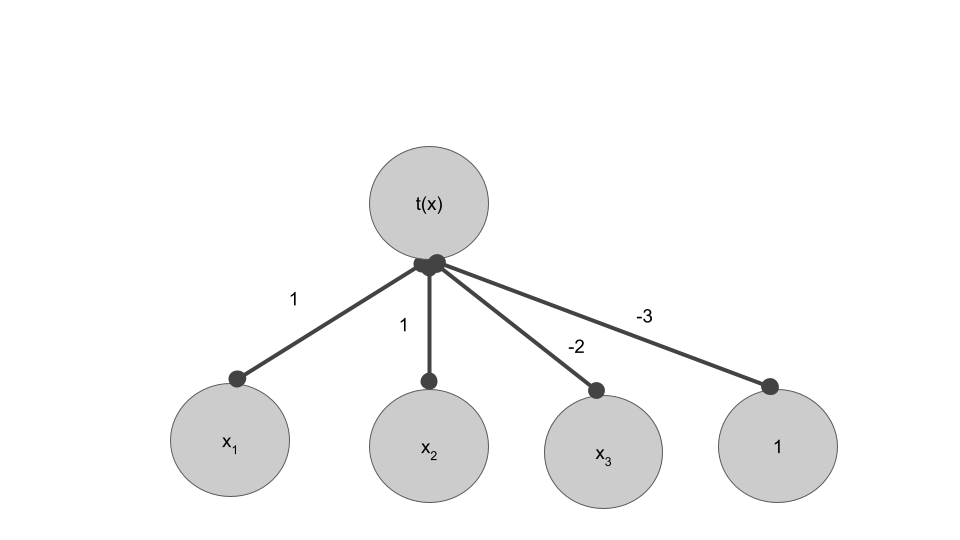
• Your input is $[-1, -2, 3]$ and your desired output is 1

Question: What is your current model's prediction

Question: How should we update our weights

Chain Rule of Calculus and Derivation of Perceptron Learning Rule

• Recall (or learn) the chain rle of calculus.

  • Suppose we have a function $F(x) = f(g(x))$
  • The derivative of $F(x)$ wrt $x$ is defined as $$ F'(x) = f'(g(x))g'(x)$$
  • if we define $y = f(u)$ and $u=g(x)$ then we can express this derivative as $$ \frac{d_y}{d_x} = \frac{d_y}{d_u} \frac{d_u}{d_x} $$

• Suppose $R(z) = \sqrt{5z-8}$

• Further, consider

  • $f(u) = \sqrt{u}$
  • $f'(u) = \frac{1}{2}\sqrt{u}^{-\frac{1}{2}}$
  • $g(z) = 5z-8$
  • $g'(z) = 5$

Question Use the chain rule to find $R'(z)$

Question Consider $R(x) = g(x)^n$. Work through the chian rule to give an expression for $R'(x)$

Question: Derive our update rule. Consider a modified MSE cost function

$$L = \frac{1}{2m}\sum_{i=1}^m (y^{(i)}-\hat{y}^{(i)})^2 $$

• To derive our update rule, do the following

1. Recall the general form (using $w_i$) for our forward pass
2. Use chain rule to find $\frac{\partial L}{\partial w_1}$, $\frac{\partial L}{\partial w_2}$, $\frac{\partial L}{\partial w_3}$, $\frac{\partial L}{\partial b}$. Note, ignore $t()$ when calculating gradients.
3. Change weights ($w_1$, $w_2$, $w_3$, $b$) in accordance to your findings (assuming a learning rate of 1)

Backward and Backpropagation

• Consider this multi-layer neural network, graphed here eliding connection weight labels and the bias for visual simplicity

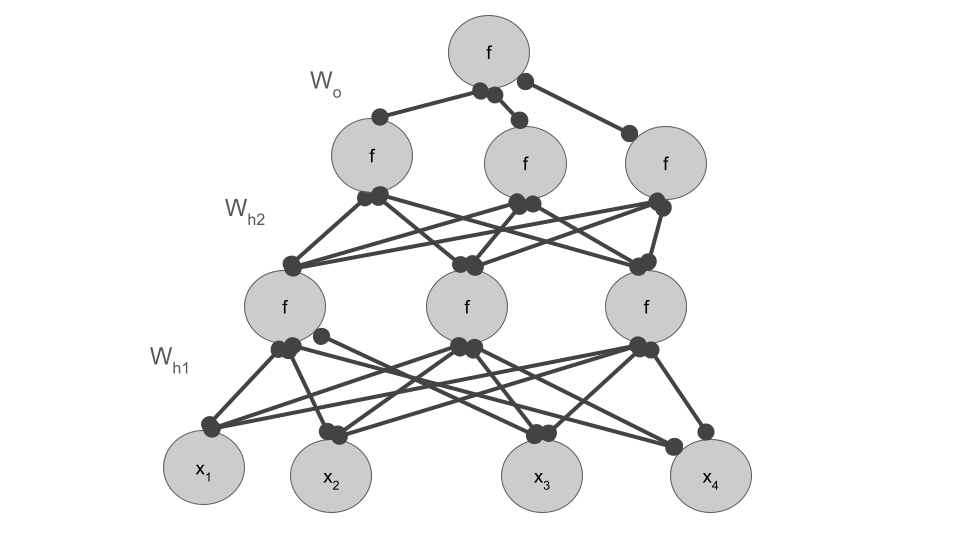
Question GIve the general expression for this network assuming,

• $W_{h_1}$ is the weight matrix mapping input to hidden layer 1
• $W_{h_2}$ is the weight matrix mapping hidden layer 1 to hidden layer 2
• $W_{o}$ is the weight matrix mapping hidden layer 2 to the output
• and $b_{h_1}$, $b_{h_2}$, $b_{h_2}$ are the relevant biases

Question: Calculate the gradient wrt to $W_{h_o}$, $W_{h_2}$, $W_{h_1}$.

Hints:

• Treat $W_{h_o}$, $W_{h_2}$, $W_{h_1}$ as if they were scalars
• First tell me $\frac{\partial z}{\partial w}$ where $z = 3f(g(wx+4)+6)$

Question Beyond this being tediuous, what are some computational limitations in updating each parameter (e.g., $W_o$) by evaluating these expressions? Consider what you have to compute.

Question Consider the following modified version of $\frac{\partial O}{\partial W_{h_2}}$. Tell me what A, B, C, A', B', and C' expand to and give me the modified versions of $\frac{\partial O}{\partial W_{h_1}}$ and $\frac{\partial O}{\partial W_{o}}$.

$$\frac{\partial O}{\partial W_{h_2}} = A'W_oB'C $$

Question Reconsider our graph. Label it with where A, B, and C are calculated.

Question Finally, let's add in our loss (modified MSE for now)

$$L = \frac{1}{2m}\sum_{i=1}^m (y^{(i)}-\hat{y}^{(i)})^2 $$

Tell me $\frac{\partial L}{\partial W_o}$

Question Can you think of a better algorithm for calculating the gradients without repeating computations? Consider when you know A, B, C.

You just derived Backpropagation!