Decision Trees and Random Forests

Prof. Forrest Davis

Apply a decision tree to new data

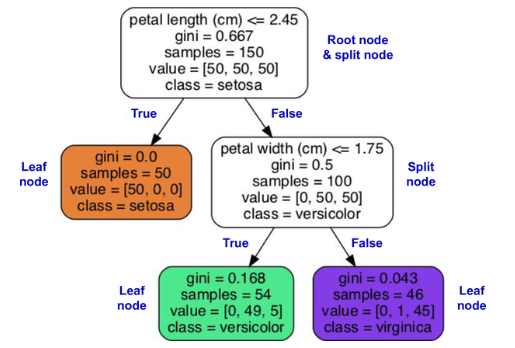
• Consider the following decision tree (from the book).

Question: Classify a new data point with the following values:

• petal length: 2.50cm
• petal width: 1.75cm

Step One: A classification problem (our old friend, the bad plots)

• Consider the following figure.

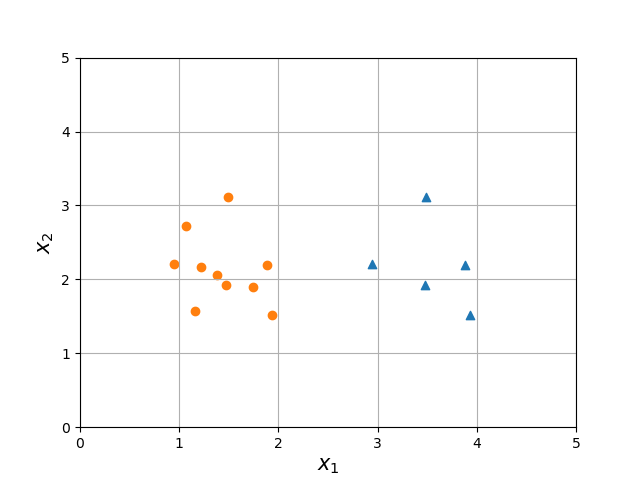
Question: Calculate the Gini impurity.

• Hint: You can get the Gini impurity if you can answer the following question:

  • What is the probability of classifying a point incorrectly (e.g., if I select a triangle, and I guessed based on the labels I know exist, what is the likelihood I misclassify a triangle)?

Step Two: Apply Gini impurity

• Consider the following two potential decision boundaries:

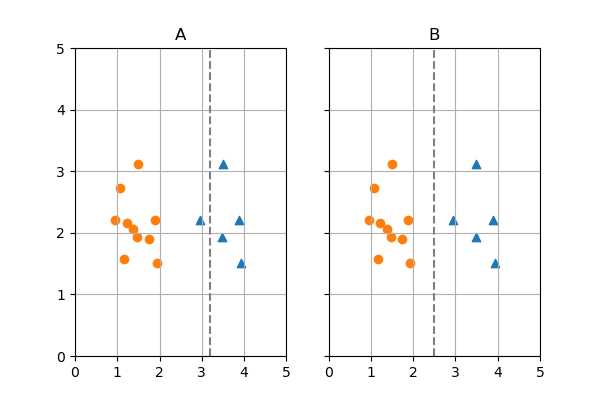
Question: Calculate the Gini impurity for the left and right regions for each decision boundary

Question: Calculate the CART cost function value for both decision boundaries

Question: How much information did I gain with each decision bounday?

• Consider a binary classification task. Three decision boundaries with the following properties are generated. Determine their Gini values.

  • All points belong to class 1
  • Half of the points belong to class 1
  • None of the points belong to class 1

Step Three: CART Algorithm Sketch

Guiding Questions:

• Sketch out the CART Algorithm
• Why is this algorithm greedy?
• What are possible stopping criteria?

Learning a decision tree for continuous data

• Given the following sample data, use the CART algorithm to learn a decision tree.

Sample	F$_1$	Y
1	2.2	1
2	3.2	0
3	4.2	0
4	4.6	1
5	5.6	1

Learning a decision tree for non-binary categorical data

Question

• Given the following sample data, use the CART algorithm to learn a decision tree.

Sample	F$_1$	F$_2$	Y
1	A	cat	1
2	B	cat	1
3	A	cookie	0
4	C	cookie	0
5	C	dog	0
6	B	dog	1
7	A	cat	1

Limitations of Decision Trees

Question What are some limitations of decision trees?

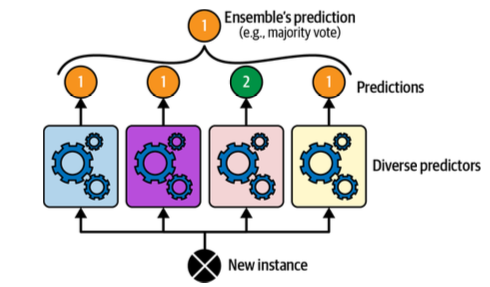
Random Forests, Ensemble Learning, and Voting Classifiers

• Random forests: train a bunch of decision trees on your data (adding in some randomness to ensure differences between each decision tree).
• Ensemble learning: train a bunch of models and use them all to make a prediction
• Voting Classifiers is one approach to ensemble learning.